L'analisi di un trend, con misurazioni stagionale, o generalmente cicliche, non può essere misurata con una semplice regressione lineare sui dati di cui disponiamo, se non siamo certi che questi dati siano indipendenti dal periodo di tempo in cui sono stati registrati. Per fittare un modello più preciso occorre quindi tenere presente anche dell'importante dato della stagionalità, e aggiustare il modello di conseguenza (si parla di seasonal adjustment.
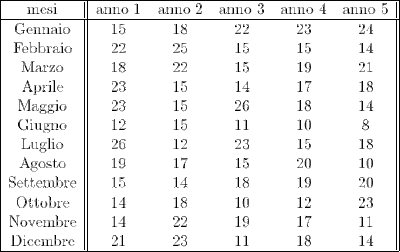
Osserviamo ad esempio i dati seguenti, che si riferiscono alle misurazioni effettuate nelle 4 stagioni per 5 anni successivi (totale 5x4 = 20 osservazioni):
21, 16, 11, 19, 25, 19, 14, 22, 29, 23, 20, 26, 33, 27, 22, 30, 36, 29, 23, 33
Ovviamente non possiamo continuare la nostra disamina senza seguire il consiglio di Chatfield (si sa, l'occhio umano vede molto più in un grafico di qualsiasi computer al mondo!):
x <- c(1:20)
y <- c(21, 16, 11, 19, 25, 19, 14, 22, 29, 23, 20, 26, 33, 27, 22, 30, 36, 29, 23, 33)
plot(x, y, type="l")

E' evidente come l'andamento dei dati dipenda dalla stagione. Fittiamo il modello e disegnamo la retta di regressione:
fit <- lm(y ~ x)
abline(fit, col="red", lwd=2)
summary(fit)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-7.6361 -2.0744 0.1662 2.4632 7.1188
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.5789 2.2066 7.060 1.39e-06 ***
x 0.7925 0.1842 4.302 0.000429 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.75 on 18 degrees of freedom
Multiple R-squared: 0.507, Adjusted R-squared: 0.4796
F-statistic: 18.51 on 1 and 18 DF, p-value: 0.000429

L'equazione della retta di regressione è: y = 15.5789 + 0.7925x. Sia l'intercetta, sia il coefficiente di regressione b sono significativi. Ma il multiple R-squared è molto basso, solo del 50.7%. Ciò ci obbligherebbe a rifiutare il modello, essendo insufficientemente adeguato.
Ora, creiamo un vettore contenente i valori predetti dalla retta di regressione, che possono essere facilmente calcolati andando a sostituire i valori delle x nella equazione della retta di regressione trovata. In R si può usare comodamente la funzione
predict():val_pred <- predict(fit)
Adesso sottraiamo ai valori reali (vettore
y), i valori predetti dalla equazione (vettore val_pred), ottenendo così un vettore contenente i cosiddetti valori de-trended:de_trended <- y - val_pred
Adesso riarrangiamo questi valori al fine di ottenere una tabella a doppia entrata: anno e valore de-trended per ogni quarto. Notate che il 1° quarto, dei 5 anni, è contenuto nelle caselle 1, 5, 9, 13, 17; il 2° quarto nelle caselle 2, 6, 10, 14, 18; e così via.
stag <- matrix(de_trended,ncol=4,byrow=TRUE)
colnames(stag) <- c("Quarto1","Quarto2","Quarto3","Quarto4")
rownames(stag) <- c("Anno1","Anno2","Anno3","Anno4","Anno5")
stag <- as.table(stag)
stag
Quarto1 Quarto2 Quarto3 Quarto4
Anno1 4.6285714 -1.1639098 -6.9563910 0.2511278
Anno2 5.4586466 -1.3338346 -7.1263158 0.0812030
Anno3 6.2887218 -0.5037594 -4.2962406 0.9112782
Anno4 7.1187970 0.3263158 -5.4661654 1.7413534
Anno5 6.9488722 -0.8436090 -7.6360902 1.5714286
Per calcolare la media di ogni colonna (ossia la media delle misurazioni per ogni stagione), procediamo così:
mediacol <- colMeans(stag)
mediacol
Quarto1 Quarto2 Quarto3 Quarto4
6.0887218 -0.7037594 -6.2962406 0.9112782
Adesso trasformiamo in vettore questi dati, e poi creiamo un vettore contenente le medie, ripetuto 5 volte (quanto il numero di anni):
mediacolvec <- as.vector(mediacol)
stag_means <- rep(mediacolvec, 5)
Ora creiamo il vettore differenza tra i dati misurati (vettore
y) e le medie stagionali (vettore stag_means):
ValAdj <- y - stag_means
Infine ricaviamo i valori residui, sottraendo ai valori misurati (vettore
y) le medie stagionali (vettore stag_means) e i valori predetti dal modello (vettore val_pred):
residuals <- y - stag_means - val_pred
Può essere utile riunire tutti i dati calcolati fino ad ora in un unico dataframe:
data <- data.frame(x, y, val_pred, de_trended, stag_means, ValAdj, residuals)
data
x y val_pred de_trended stag_means ValAdj residuals
1 1 21 16.37143 4.6285714 6.0887218 14.91128 -1.4601504
2 2 16 17.16391 -1.1639098 -0.7037594 16.70376 -0.4601504
3 3 11 17.95639 -6.9563910 -6.2962406 17.29624 -0.6601504
4 4 19 18.74887 0.2511278 0.9112782 18.08872 -0.6601504
5 5 25 19.54135 5.4586466 6.0887218 18.91128 -0.6300752
6 6 19 20.33383 -1.3338346 -0.7037594 19.70376 -0.6300752
7 7 14 21.12632 -7.1263158 -6.2962406 20.29624 -0.8300752
8 8 22 21.91880 0.0812030 0.9112782 21.08872 -0.8300752
9 9 29 22.71128 6.2887218 6.0887218 22.91128 0.2000000
10 10 23 23.50376 -0.5037594 -0.7037594 23.70376 0.2000000
11 11 20 24.29624 -4.2962406 -6.2962406 26.29624 2.0000000
12 12 26 25.08872 0.9112782 0.9112782 25.08872 0.0000000
13 13 33 25.88120 7.1187970 6.0887218 26.91128 1.0300752
14 14 27 26.67368 0.3263158 -0.7037594 27.70376 1.0300752
15 15 22 27.46617 -5.4661654 -6.2962406 28.29624 0.8300752
16 16 30 28.25865 1.7413534 0.9112782 29.08872 0.8300752
17 17 36 29.05113 6.9488722 6.0887218 29.91128 0.8601504
18 18 29 29.84361 -0.8436090 -0.7037594 29.70376 -0.1398496
19 19 23 30.63609 -7.6360902 -6.2962406 29.29624 -1.3398496
20 20 33 31.42857 1.5714286 0.9112782 32.08872 0.6601504
Adesso creiamo il modello con i valori aggiustati tenendo conto della stagionalità (vettore
ValAdj):
fitAdj <- lm(ValAdj ~ x)
summary(fitAdj)
Call:
lm(formula = ValAdj ~ x)
Residuals:
Min 1Q Median 3Q Max
-2.01489 -0.34255 -0.07942 0.35628 1.96029
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.74507 0.37554 39.26 < 2e-16 ***
x 0.87190 0.03135 27.81 3.05e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.8084 on 18 degrees of freedom
Multiple R-squared: 0.9773, Adjusted R-squared: 0.976
F-statistic: 773.5 on 1 and 18 DF, p-value: 3.048e-16
Osservate il valore di multiple R-squared: questo modello così creato ha un valore molto più elevato, addirittura del 97.73%.
Disegnamo anche la retta di regressione aggiustata, e osserviamo il grafico:
abline(fitAdj, lwd=2, col="blue")
text(max(x)-1.5, max(predict(fit))-2, paste("Without seas adj"), pos=1, col="red")
text(max(x)-3.1, max(predict(fitAdj)), paste("With seas adj"), pos=1, col="blue")